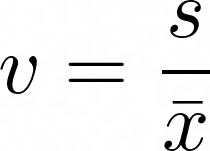Auf dieser Seite finden sich zahlreiche statistische Formeln als hochauflösende Grafiken mit transparentem Hintergrund sowie als LaTeX-Code zur freien Nutzung. Die Zusammenstellung wird laufend erweitert. Enjoy!
Additionssatz für beliebige Ereignisse
P(A \cup B)=P(A)+P(B)-P(A \cap B)
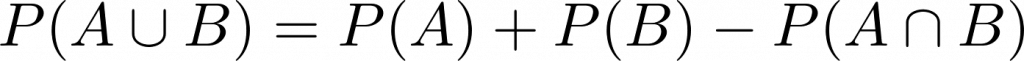
Additionssatz für unvereinbare Ereignisse
P(A \cup B)=P(A)+P(B)
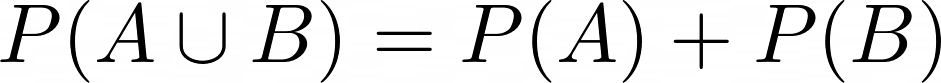
Arithmetisches Mittel
\bar x = \frac{1}{n} \sum\limits_{i=1}^{n}x_i
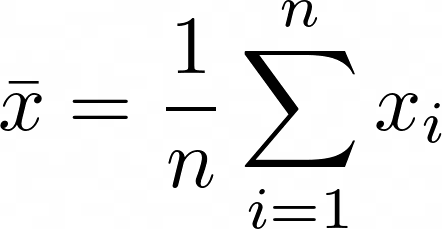
Arithmetisches Mittel bei klassierten Daten
\bar x_g = \sum\limits_{i=1}^{k}(m_i f_i)
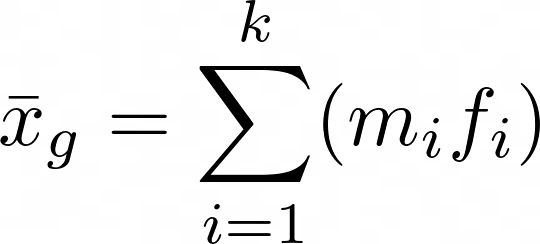
Bravais-Pearson-Korrelationskoeffizient
r = \frac{\sum\limits_{i=1}^{n}(x_i y_i)-n \bar{x} \bar {y}}{\sqrt{\sum\limits_{i=1}^{n}(x_i^2)-n \bar x^{2}}\sqrt{\sum\limits_{i=1}^{n}(y_i^2)-n \bar y^{2}}}
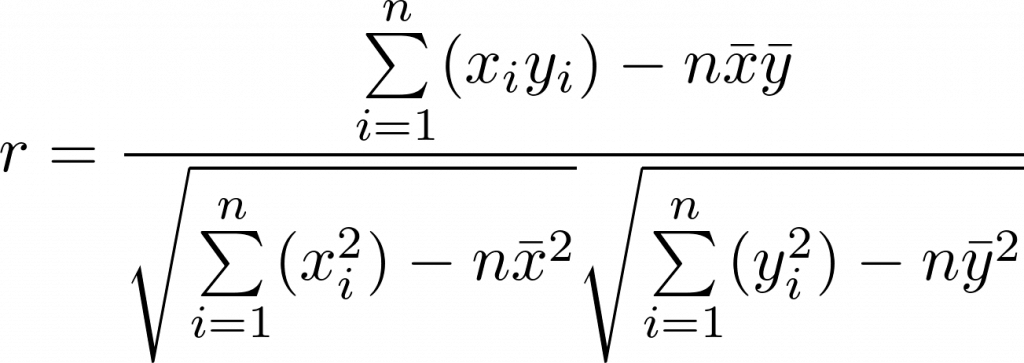
Cochran-Formel
n= \frac{\frac{Z^2 p q}{e^2}}{1+\frac{\frac{Z^2 p q}{e^2}-1}{N}}
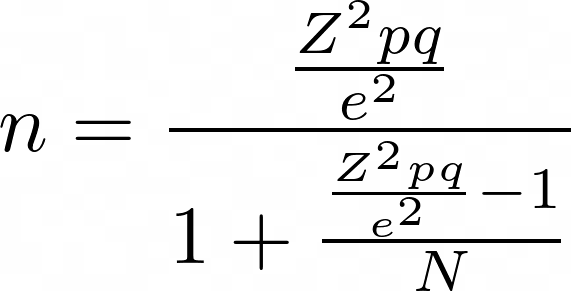
De-morgansche Regeln
\overline{(A \cup B)}= \bar{A} \cap \bar{B}\\
\overline{(A \cap B)}= \bar{A} \cup \bar{B}
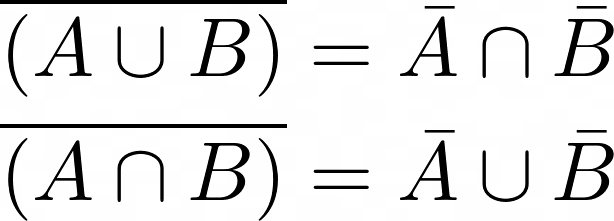
Erstes Axiom von Kolmogoroff
P(A) \geq 0
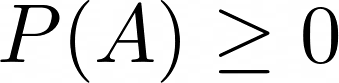
Zweites Axiom von Kolmogoroff
P(\Omega) = 1
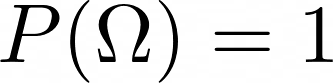
Drittes Axiom von Kolmogoroff
P(A \cup B) = P(A) + P(B)
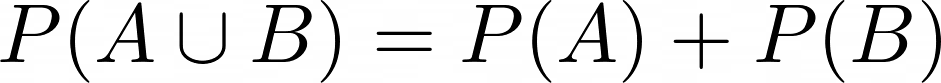
Empirische Varianz
s^2 = \{ \frac{1}{n} \sum\limits_{i=1}^{n}x_i^2 \} – \bar{x}^2
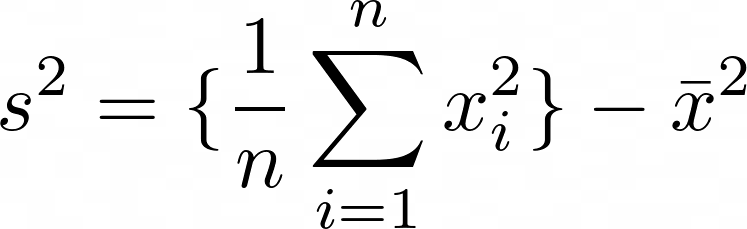
Fünf-Werte-Zusammenfassung
[x_{min};x_{0,25};x_{med};x_{0,75};x_{max}]
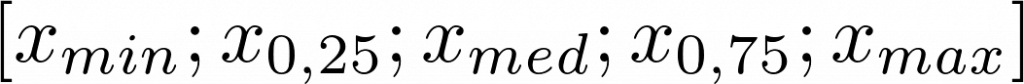
Geometrisches Mittel
\bar x_{geom} = \sqrt[n]{x_1…x_n}
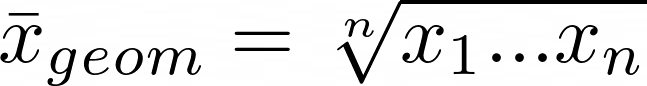
Getrimmtes arithmetisches Mittel
\bar x = \frac{1}{n} \sum\limits_{i=1}^{n}x_i
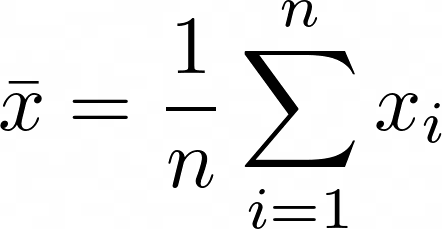
Gütemaß der univariaten linearen Regressionsanalyse
R^2 = \frac{ESS}{TSS}
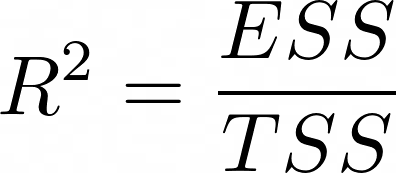
Harmonisches Mittel
\bar x_{har} = \frac{n}{\sum\limits_{i=1}^{n}{\frac{1}{x_i}}}
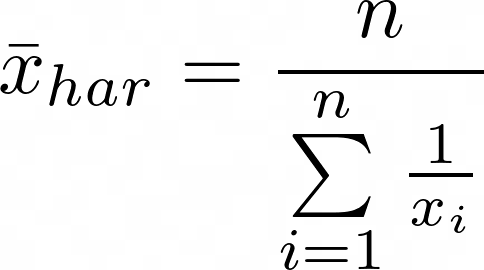
IQR
IQR = x_{0,75}-x_{0,25}
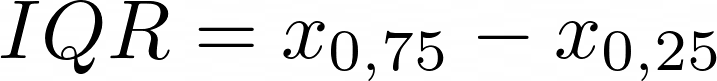
Konkordanzkoeffizient nach Kendall
tau = \frac{2(K-D)}{n(n-1)}
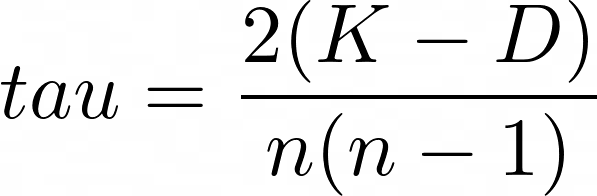
Klassiertes Mittel
\bar x_g = m_1 f_1 + … + m_k f_k \sum\limits_{i=1}^{k}{m_i f_i}
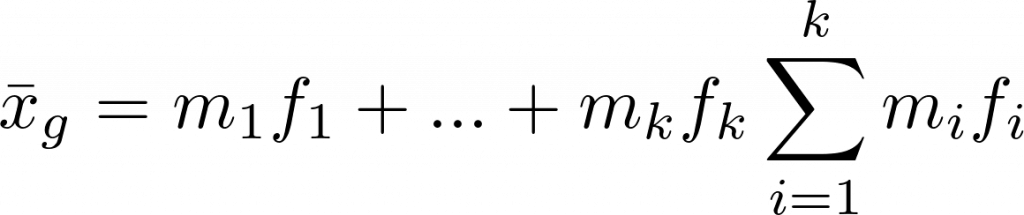
Kombination mit Zurücklegen
\frac{(n+k-1)!}{(n-1)!k!}
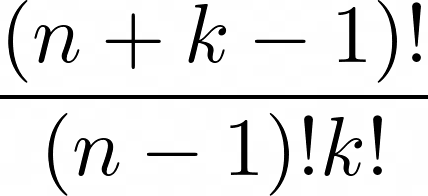
Kombination ohne Zurücklegen
\frac{n!}{k!(n-k)!}
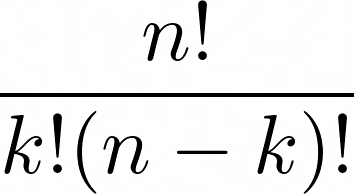
Konfidenzintervall um my
P(\bar x – z_{1-\frac{\alpha}{2}} \frac{\sigma}{\sqrt{n}} \leq \mu \leq \bar x + z_{1-\frac{\alpha}{2}} \frac{\sigma}{\sqrt{n}} ) = 1-\alpha
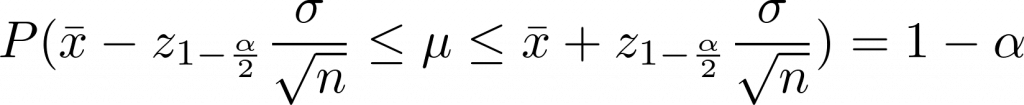
Konfidenzintervall um p
P(\hat p – z_{1-\frac{\alpha}{2}} \sqrt{\frac{\hat p (1 – \hat p)}{n}} \leq p \leq \hat p + z_{1-\frac{\alpha}{2}} \sqrt{\frac{\hat p (1 – \hat p)}{n}}) = 1-\alpha
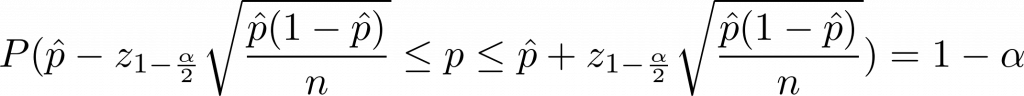
Konstantes Glied aus der univariaten linearen Regressionsanalyse
a = \bar y – b \bar x
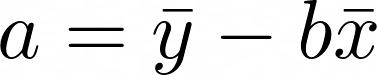
Kurtosis
g_k = \frac{m_4}{s^4}-3\\
m_4 = \frac{1}{n} \sum\limits_{j=1}^{n}({x_j – \bar x})^4\\
s^4 = \Biggl(\sqrt{\frac{1}{n} \sum\limits_{i=1}^{n}(x_i – \bar x)^2}\Biggl)^4
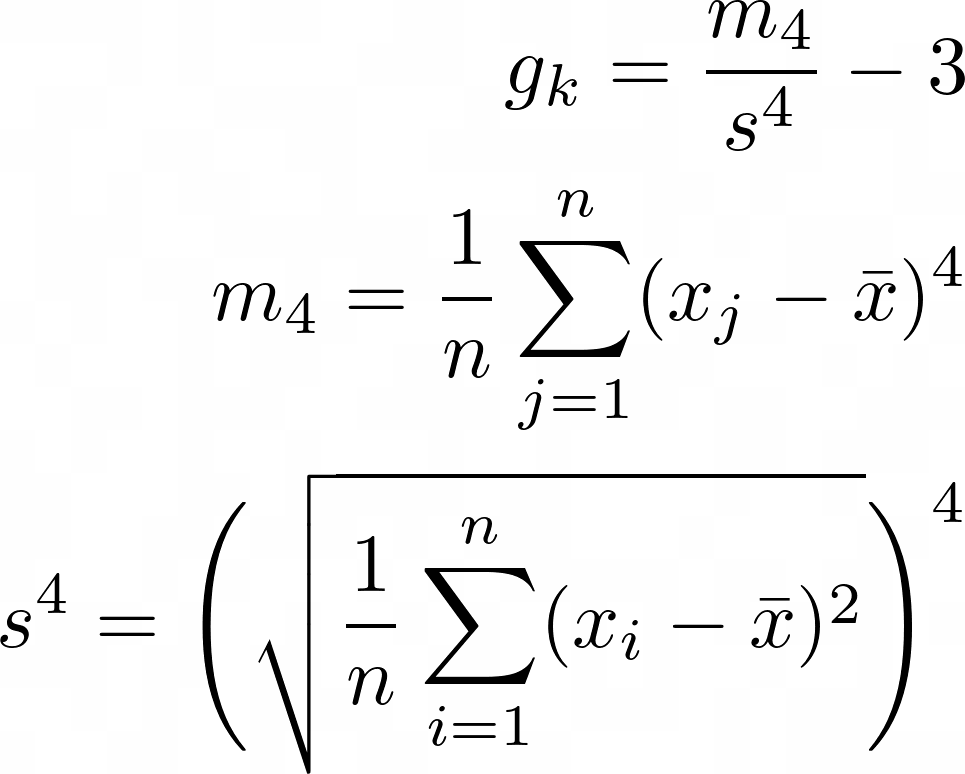
Laplace-Wahrscheinlichkeit
P(A) = \frac{\sum{zu \, A \, passende \, Elementarereignisse}}{\sum{denkbare \, Elementarereignisse}}
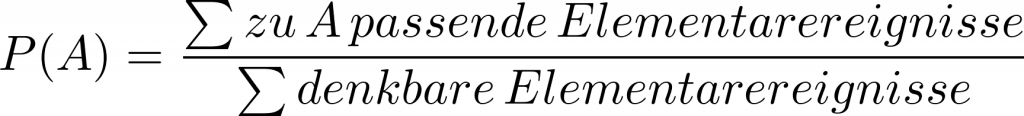
Median bei gerader Anzahl von Werten
x_{med} = \frac{1}{2}(x_{(\frac{n}{2})}+x_{(\frac{n}{2}+1)})
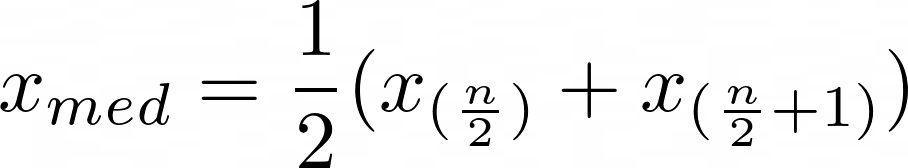
Median bei ungerader Anzahl von Werten
x_{med} = x_{(\frac{n+1}{2})}
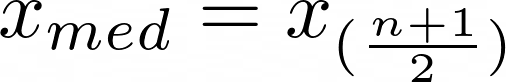
Modus
x_{mod} = a_{x \, max}
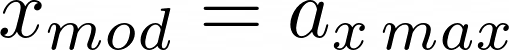
Momentenkoeffizient der Schiefe
g_m = \frac{m_3}{s^3}\\
m_3 = \frac{1}{n} \sum\limits_{i=1}^{n}({x_i – \bar x})^3\\
s^3 = \Biggl(\sqrt{\frac{1}{n} \sum\limits_{i=1}^{n}(x_i – \bar x)^2}\Biggl)^3
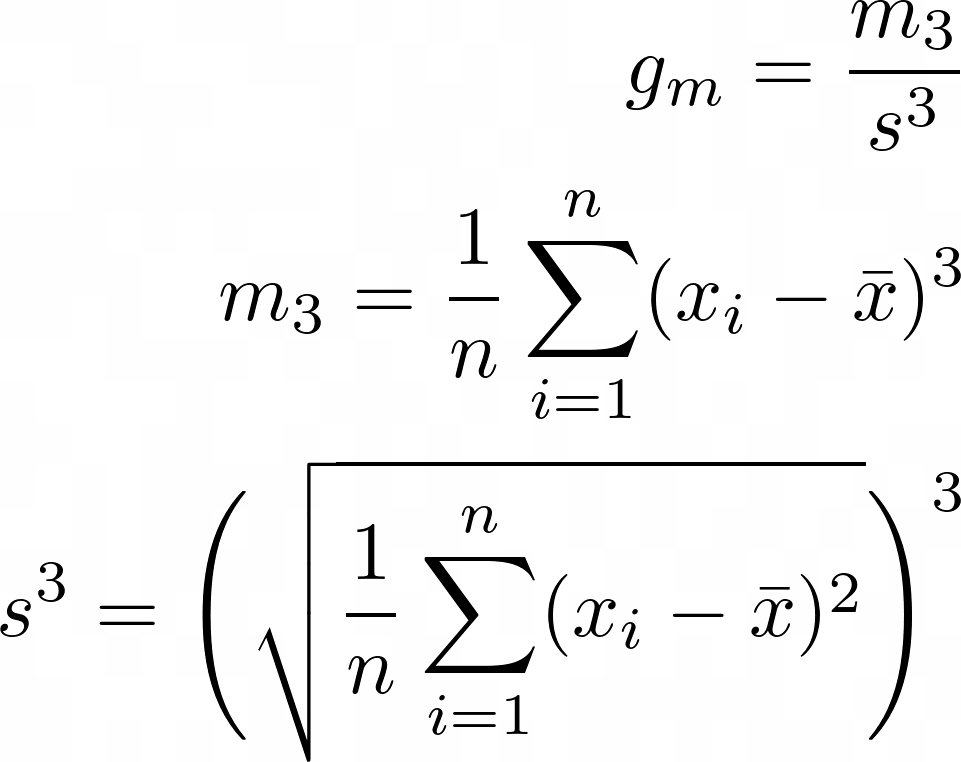
Multiplikationssatz für unabhängige Ereignisse
P(A \cap B) = P(A) P(B)
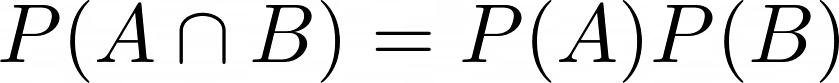
Perzentil bei ganzzahligem np
x_p = \frac{1}{2}(x_k + x_{(k+1)})
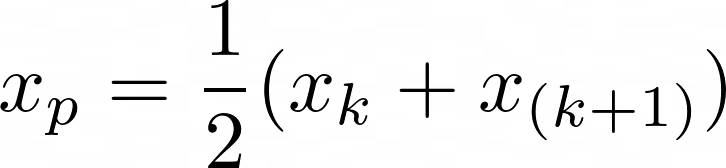
Perzentil bei nicht ganzzahligem np
x_p = x_k
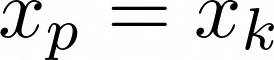
Quartilskoeffizient der Schiefe
g_{0,25} = \frac{(x_{0,75}-x_{med})-(x_{med}-x_{0,25})}{x_{0,75}-x_{0,25}}
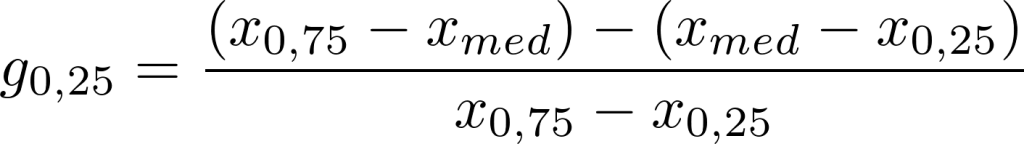
Regressionsfunktion der univariaten linearen Regressionsanalyse
y = a + b x
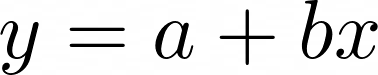
Regressionskoeffizient der univariaten linearen Regressionsanalyse
b = \frac{\sum\limits_{i=1}^{n}(x_i y_i)-n \bar x \bar y}{\sum\limits_{i=1}^{n}(x_i^2)-n \bar x^2}
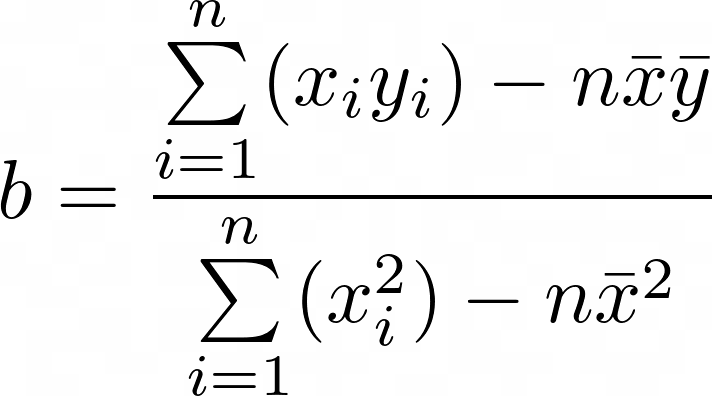
Satz der totalen Wahrscheinlichkeit
P(B) = \sum\limits_{i=1}^{k}P(B|A_i) P(A_i)
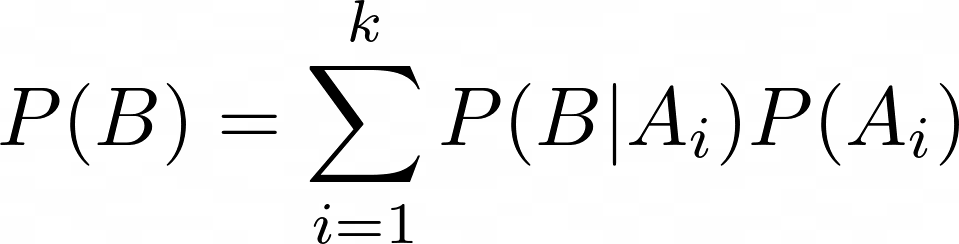
Satz von Bayes
P(A_i|B)=\frac{P(B|A_i) \, P(A_i)}{P(B)}
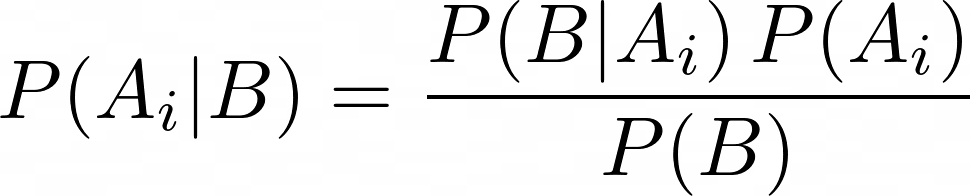
Spannweite
d_s = x_{max}-x_{min}
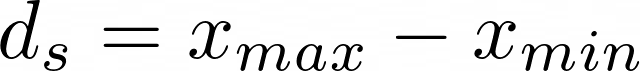
Rangkorrelationskoeffizient nach Spearman
rho=1-\frac{6 \sum d_i^2}{(n^2-1)n}
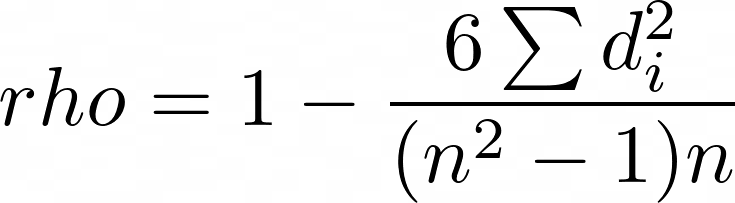
Standardabweichung
s = + \sqrt{s^2}
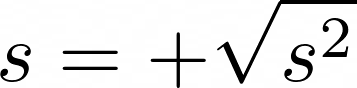
Stichprobenvarianz
s^2 = \frac{1}{(n-1)} \sum\limits_{i=1}^{n}(x_i – \bar x)^2
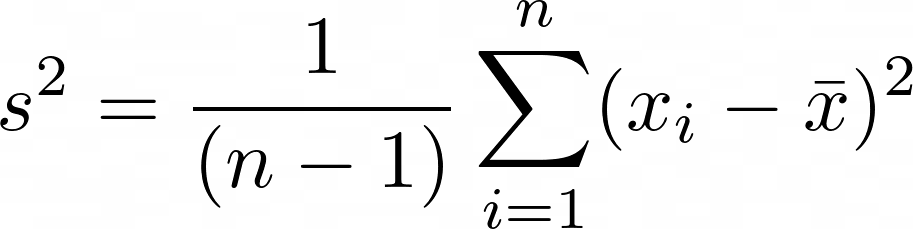
Varianz
s^2=\frac{1}{n}\sum\limits_{i=1}^{n}(x_i-\bar x)^2
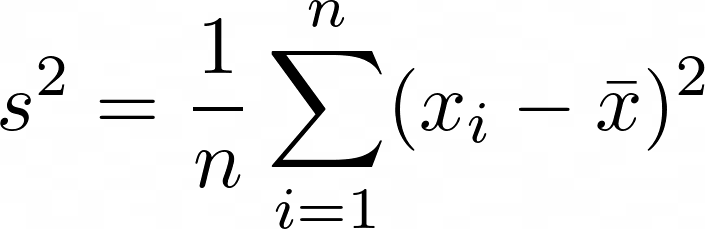
Variation mit Zurücklegen
n^k
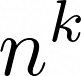
Variation ohne Zurücklegen
\frac{n!}{(n-k)!}
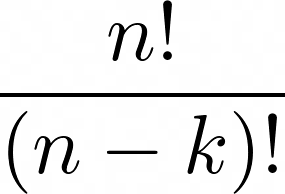
Variationskoeffizient
v=\frac{s}{\bar x}